抛开复杂的理论,直探事物的本质。
这是这个主题的第三篇文章,前两篇介绍了这几种码的基本概念,这篇文章来具体说说「移码」。
00. 回顾
先来回顾一下移码是什么,简单说定义就一句话:将补码符号位取反,即为移码。乍一看,是不是有点懵,这到底在说什么呢?什么是移码?为什么是这么算?它能干嘛用?莫急,这些问题一个一个都会解决。
相比于移码,应该使用补码的几率更高一些。因为移码主要用在浮点数的阶码中,用的较少。注意,这里又出来了一个新名词,「阶码」,关于这块的内容比较乱,会单独写一篇文章来说。而现在只需要记住一句话,移码的出现就是为了消灭负数。
01. 如何「消灭」负数
先拿大家都熟悉的数轴举个例子。
如图,数轴上一共有 5 个点,分别为 -2、-1、0、1、2,其中有 2 个负数,所谓消灭负数,就是用 5 个非负数来表示这 5 个点,方法就是将 0 向左移动两个位置,如下。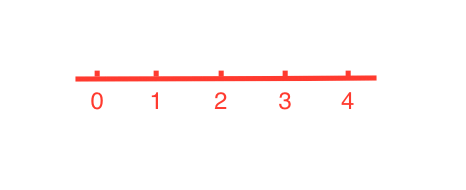
很简单吧,这样一移动负数就被消灭了,而「移码」的计算就是这个道理,而将 0 向左移动 2 个位置就等同于将所有数字加 2,这个很好理解。很显然,移动的位数就是表示范围内负数的个数。
02. 为什么是补码符号位取反?
先明确一点:因为移码都是非负数,不需要符号位,所以,所有的二进制位都是用来表示数据的。
接下来,根据上面得出的结论,我们亲自来算一算移码。为了便于计算,就拿 4 位二进制来举例。在计算机中,4 位二进制能表示的范围为 [-2^3, 2^3-1] = [-8, 7],其中负数的个数为 -1 到 -8,共 2^3 个,也就是 8 个,所以需要将 0 向左移动 8 个位置,即给每个数加上 8,如下。
1 | 补码 +8 移码 |
上面这样对比着看,应该很清晰了。经过计算得出的移码,刚好等于补码符号位取反,所以移码的定义就简化成了一句话:将补码符号位取反,即为移码。
再说一个有点不好理解的方法,觉得啰嗦略过就好。除去首位的符号位不看,单看剩下的 3 位二进制,-8 到 -1 本身就符合从小到大的规律,而 0 到 7 也是如此,但 [0,7] 要大于 [-1,-8],强转成无符号数,用符号位的 0 和 1 两个值便可以区分原本的 8 个负数和 8 个非负数,最终就是将负数转化为了正数,将正数转化为了更大的正数。
结束
至此,关于「原码 反码 补码 移码」主题的文章就告一段落了。
段首写了这么一句话:「抛开复杂的理论,直探事物的本质」。我是这么理解这句话的,讲一样东西,只有把没什么基础的人都说明白了,说懂了,也不用过多的摆理论、套公式,这样才算是真的讲透彻了,话虽俗,理不俗。