理解矩阵乘法

大学时候有一门叫做线性代数的课程，虽然没挂科，但是好像就没学明白过，直到最近在看的计算机图形学，涉及到了相关内容，这么多年没明白的东西，突然好像就明白了。

谷歌上搜索，矩阵乘法的本质是什么，一定会看到这样的答案：线性变换的复合。一个直观看上去很抽象的回答，直到看到这个通俗的解释后，恍然大悟的感觉。

知乎上面看到的，我没登录所以只让看这么多，后面的不让看了，不过这些就已足够。

原回答在这里：矩阵乘法的本质是什么？ - 知乎用户的回答 - 知乎

用他的话来说就是：我们管这种从材料列表转为开销表的过程，就叫做一个线性映射。这也即是矩阵乘法的意义。

乘法拆分

这样看更直观一些，但是只适用于右侧是一列的矩阵，也可叫做向量。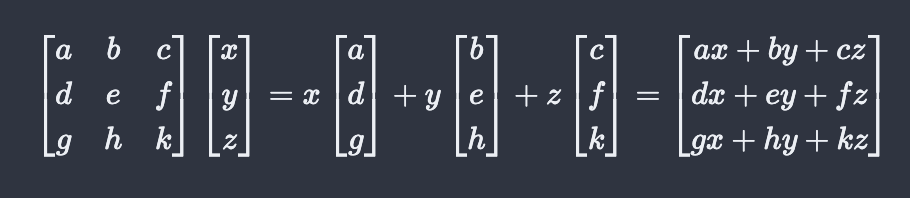

$$\begin{bmatrix}
a&b&c\
d&e&f\
g&h&k\
\end{bmatrix}
\begin{bmatrix}
x\
y\
z\
\end{bmatrix}
=
x
\begin{bmatrix}
a\
d\
g\
\end{bmatrix}
+
y
\begin{bmatrix}
b\
e\
h\
\end{bmatrix}
+
z
\begin{bmatrix}
c\
f\
k\
\end{bmatrix}
=
\begin{bmatrix}
ax+by+cz\
dx+ey+fz\
gx+hy+kz\
\end{bmatrix}
$$

关于相乘的过程，有个网站做了个动画，这种形式更加清晰。

矩阵乘法动画

理解较为初级，所以写的很粗躁，可作为入门笔记。

参考

• How to Multiply Matrices
• 理解矩阵乘法
• 二维几何变换
• Markdown中插入矩阵乘法